A few years ago, I made a crossword-like game wherein users fill out a 4×4 grid of letters to spell 8 words (4 across and 4 down): http://osric.com/chris/wordgame/
However, over the course of several days, I was able to develop only 20 puzzles by hand. Trying all the various combinations is clearly a task better suited to computers than humans. Such a grid has 16 slots, each of which can contain one of 26 letters–so there are 2616 total permutations to check. That’s about 43,000,000,000,000,000,000,000–which could take a very long time, even for a computer. One key to speeding things up is to ignore permutations that don’t contain words.
First I tried using the default dictionary file on my computer (/usr/share/dict/words on Mac OSX), which contains around 4000 4-letter words. I could test all of the permutations of words, placing them a word in each row of the 4×4 grid and then testing the letters in the grid columns to see if they are dictionary words. This reduces the problem to 40004 (~26 trillion), which could still take a very, very long time.
Such a program isn’t very smart, though. Let’s say it checked this grid:
| B | A | B | Y |
| B | A | T | S |
| B | A | L | K |
| B | A | N | K |
After discovering that BBBB isn’t in the dictionary, it would proceed by replacing BANK with BANS and failing on the same non-word, BBBB. In fact, as soon as it inserts BATS after BABY, it should check and discover than no dictionary word begins with BB, and skip to CABS, then DABS, then EACH–where it finally finds a valid word prefix, BE. We “pruned” B, C, and D. The dictionary file has about 700 words that begin with B, C, or D–so the pruning just eliminated 700 x 4000 x 4000, or 11 billion permutations.
Following this strategy, I created a program in Java to test various permutations but bypass permutations that lead to invalid word prefixes. It looked like it was running properly, but would probably take several days to complete. Additionally, many of the words in the dictionary were uncommon and were creating grids unfriendly for a casual puzzle game (like ACYL).
I was using the Eclipse IDE for this project, and I noticed that most of the unusual words in my list were underlined in red. Eclipse didn’t recognize them as words! Eclipse must have its own dictionary. It took me a while to find it, but eventually I:
- Grabbed the Eclipse dictionary from http://dev.eclipse.org/viewsvn/index.cgi/org.eclipse.jdt.ui/dictionaries/en_US.dictionary?view=co
- Reduced it to the 4-letter entries
cat en_US.dictionary | grep '^[a-zA-Z]\{4\}$' > 4letters.dictionary - Sorted it alphabetically (ignoring case)
sort -f -u 4letters.dictionary -o sorted4.dictionary
The new file contained 1788 words–a smaller list with more recognizable words. This time, my program ran to completion in 5295 seconds (about an hour and a half) and found 498,672 4×4 grids where all the words, across and down, were in the dictionary file! Nearly half a million grids, when I was stuck after coming up with 20 by hand!
Many of the grids contained the same word more than once, though, e.g.:
| Z | O | N | E |
| O | X | E | N |
| N | E | E | D |
| E | N | D | S |
That’s not a very interesting puzzle, so I added a check to exclude grids that contained the same word more than once. The updated program ran in 4734 seconds (~1 hour and 19 minutes) and found 192,476 grids.
I had an idea to speed things up further. What if, after checking the BA combinations (as in the example above), it skipped straight to EA? That’s when I had an idea to build the dictionary as a tree–my version is technically a graph, because it has an imaginary root. Each node contained a value (a word or word prefix) and pointers to a sibling or a child. For example, this is a visual representation of the graph containing ABLE, ACHE, ACHY, BAKE, BAND, and BANE:
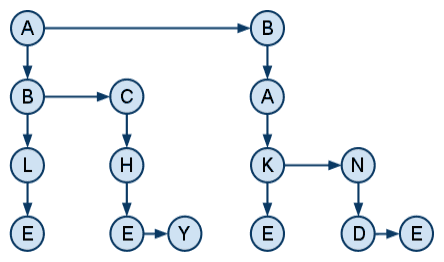
While traversing this tree, if the grid fails at a certain letter, it moves on to the next sibling. If it passes–that is, all rows and columns are either words or valid word prefixes, it moves on to the child. (This is basically Depth-First Search.) This version of the program found the same number of grids–192,476–but in only 497 seconds (8 minutes and change)!
The running time is still problematic, though. If I think of a good 4-letter addition, such as a name (“FRED”) or a phrase (as-is becomes “ASIS”), I don’t want to sit around for 8 minutes waiting to generate all the puzzles again. I could address this by testing only grids that contain the new additions, which should run in a blink.
Also, the successful grids include isomorphic grids. For example,
|
and |
|
This isn’t really a tremendous problem, though–a player is unlikely to run into 2 isomorphic puzzles during casual game play.
Now the trick is to come up with clues for all the puzzles, and find a way to let users play on Facebook (where apparently all the casual gaming takes place anymore). For now, though, I’m content to have found a clever way to reduce the running time from 80 minutes to 8 minutes.
I shouldn’t pat myself on the back too much, though–I’m sure someone else has already found a way to do the same in mere seconds.
It is interesting that I didn’t think my graph representation was a tree (because it didn’t have a root). The labels I chose, sibling and child, threw me off–but replace child with “left child” and sibling with “right child” and it becomes apparent that the data structure is a binary tree with the root at A. I let the labels temporarily box in my way of thinking.
Would you be willing to release your source code for the block finder? I saw a clever thing I want to improve on: drink coasters made from a 4×4 grid of Scrabble letters. I have a bunch of Scrabble letters I purchased a couple of years back (don’t ask), and would love to make some coasters for our house. I was going to write a program that took a number of predefined 4×4 word grids, and checked them against the letters we have to maximize the number of coasters we can make — but I need the 4×4 grids.
If you’re not willing to reveal your code, or create a binary I could run which conceals the source code, even, I understand.
S.V.
Sure, I added the code to GitHub:
https://github.com/cherdt/fourxfour
It’s a little messy, but hopefully still useful.
Hi Chris,
I need to generate a lot of these exact word puzzles. Do you have an archive of the ones you have created somewhere?
Many thanks,
Mike
I don’t have an archive of the ones the code generated, although you are welcome to use the code to re-generate them:
https://github.com/cherdt/fourxfour
I created 20 games by hand, which are playable at 4 x 4 Puzzle.
Hey, if you have a moment I would like to seek your help with a possible isomorphic crossword puzzle we are having trouble with.
What is the grid called where downward word and across word are the same
Here’s a nice article about a similar, although far more complex, problem: identifying the Boggle board (a 4×4 grid of letters) with the highest possible score:
Lone coder cracks 50-year puzzle to find Boggle’s top-scoring board (subscription required)
Congratulations to Dan Vanderkam on finding the solution! You can also read more about the solution on Dan’s blog: After 20 Years, the Globally Optimal Boggle Board